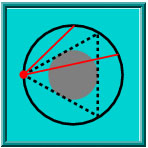
Second Solution
Since all points on the circle are equivalent, let's consider a single point, marked in red. Consider only the chords that emanate from this point. Looking at the triangle, each of whose angles is 60 degrees, it becomes clear that 1/3 of the outcomes will result in a chord longer than the side of an equilateral triangle.

Second Solution
A chord is fully determined by its midpoint. Chords whose length exceeds the side of an equilateral triangle have their midpoints inside a smaller circle with radius equal to 1/2 that of the given one. Hence, its area is 1/4 of the big circle, which also defines the proportion of favourable outcomes - 1/4.
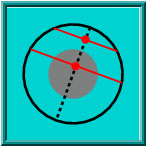
Third Solution
A chord is fully determined by its midpoint. Chords whose length exceeds the side of an equilateral triangle have their midpoints closer to the centre than half the radius. If the midpoints are distributed uniformly over the radius (instead of over the area, as was the case in the second solution), the probability becomes 1/2.
Explanation