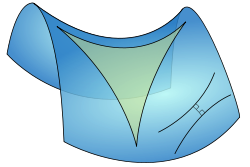

A triangle immersed in a saddle-shape plane, as well as two diverging parallel lines.
Euclid and his legacyYet there was also a counter-current. Certain mathematicians had their suspicions about the 5th Euclidean postulate, the one about parallel lines. Being more complex and less obvious than the others, it seemed more like a theorem than an axiom. So people set about trying to prove that it followed from the first four axioms. Others tried to prove the postulate by assuming its negation in the expectation that they would produce a logical contradiction. Both in vain. As it turned out in this case, failure can be as productive as success.
In modern terms, Euclid's 5th postulate is normally stated as: Given a line L and a point P not on the line, there is precisely one line through P in the plane determined by L and P that does not intersect L. The unsuccessful efforts to prove the 5th postulate of Euclid showed that many results are equivalent to it. Three such results are:
The sum of the angles in a triangle is 180 degrees.
The ratio of the circumference to the diameter of a circle is the same for all circles, regardless of size.
The Pythagorean Theorem
Non-Euclidean geometry
By 1830 it was realised that the 5th postulate was a strange beast, neither fish nor foal. For it is neither true nor false. Asked whether the 5th postulate is true or not, a modern mathematician will answer, "It depends..." It depends on the surface one is talking about. If one is doing geometry on a plane or cylindrical surface then the postulate is true. If one is performing geometrical activities on a sphere or a saddle shape then the axiom is false.
Riemann took the bold step of treating the 5th postulate not as a theorem, or axiom, nor as a true or false statement, but as a definition. This led to the birth of non-Euclidean geometry. Geometry now split into three broad classes: the geometry of positive, zero and negative curvature. The term curvature is neither abstruse nor vague. It refers to the sum of the angles of a triangle on the surface in question. If that sum is exactly 180 degrees then one is dealing with a "flat" surface, and this is the domain of application of Euclidean geometry. If the angle sum is greater than 180 degrees then one is dealing in spherical geometry. If the sum is less than 180 degrees then this is hyperbolic geometry. Equivalently, this relates to parallels. In hyperbolic geometry there are at least two distinct lines through P which do not intersect L. In spherical geometry there are no parallel lines at all.
Flat or Euclidean geometry applies to the plane and also to the surface of a cylinder. Spherical geometry applies to the surface of a sphere. Hyperbolic geometry applies to a saddle-shaped surface.
Spherical geometry
Is spherical geometry useful? It sure is, being the right one to use for the surface of the Earth. We define straight lines (geodesics) as those that travel the shortest distance between two points. On a sphere such as our Earth, geodesics are called great circles (since larger circles are not possible), each having the same diameter as the sphere. The Equator and the lines of longitude are great circles, parallels of latitude are not. Beijing and Philadelphia lie on the same latitude, and if we travelled from one to the other along this line of latitude, we would go 10,130 miles. By contrast, a geodesic between these two cities, which passes close to the North Pole, is only 6,878 miles. Yet on a flat map of the Earth the path along the line of latitude appears straight. This is because maps of the world on flat paper necessarily distort distance. This is most obvious near the North Pole, where the distance scale is distorted by a factor of about 60%.
Imagine a triangle consisting of two lines of longitude coming from the North Pole plus the segment of the Equator between them. Since the two base angles are both right angles, the sum of the angles in this triangle is more than 180 degrees. Hence geometry on a sphere has positive curvature. There are no parallel lines on a sphere, as all great circles cross one another. To see this, imagine one great circle, which cuts the sphere into two equal parts. Any other great circle cannot remain within only one of these two halves. If it did, its diameter would be less than that of the sphere.
A rectangle of cloth can be used to perfectly wrap a cylinder, which is mathematically flat. On the other hand, a sphere is not flat, so that a sheet cannot fully cover it without wrinkling. One can imagine a clever tailor fashioning a piece of cloth that will fit perfectly over the top half of a beachball. The cloth would have to have less area inside a circle of fixed radius than on a bedsheet. To do so the tailor would need to cut out darts from the fabric and then sew it together again. One would have to crease a piece of positively curved cloth to lay it on a dresser.
Hyperbolic geometry
On a hyperbolic surface there is more than one parallel line through each point P and the angles of a triangle add up to less than 180 degrees. In contrast to the sphere, whose triangles seem to bulge out, on a saddle the geodesic sides of a triangle seem sucked in. A tiny being living on either surface would view the lines as perfectly straight, and would only be able to tell whether the triangle was bulging or sucked in by measuring its angle sum.
In contrast to a sphere, the saddle-shaped area on a woman's side above her hip has negative curvature. To drape this part of her body exactly a cloth with negative curvature is required. The region inside a circle of a given radius contains more material than the same circle in a plane. To make suitable cloth a tailor might start with a flat piece of fabric, make a cut as if to make a dart, but instead of stitching the cut edges together, insert an extra piece of fabric. Negatively curved cloth has lots of folds when laid flat on a dresser.
Three dimensions, and up
The discussion so far has been limited to two dimensional geometry, ie to the study of surfaces, where there are only two independent directions. The notion of curvature extends naturally to three dimensions and beyond. The problem with discussing three dimensional geometries that are spherical or hyperbolic is that, unlike the curved surfaces mentioned above, we cannot picture or see these spaces.
For each positive integer n, an n-space is the set of all ordered n-tuples of real numbers. Euclidean space of dimension n is n-dimensional space with distance defined by the Pythagorean Theorem.
The crochet coral reef
Since hyperbolic space is not something that we can perceive directly, various models have been constructed that give us a feel for its properties. Going down one dimension, we can show what a hyperbolic surface looks like, eg a saddle shape. The crocheted coral reef is an attempt to give a feel for hyperbolic 3-dimensional space within our familiar framework of Euclidean space. The crocheted reef is a hyperbolic surface made of negatively curved cloth.
In 1997 mathematician Daina Taimina worked out how to make a physical model of hyperbolic space that allows us to feel, and to tactilely explore, the properties of this unusual geometry using crochet. The essence of the hyperbolic construction can be implemented with crochet simply by increasing the number of stitches in each row. As you increase, the surface naturally begins to ruffle and crenellate.
Many of the properties of hyperbolic space become visible to the eye and can be directly experienced by playing with the models. Geodesics on the hyperbolic surface can be sewn onto the crochet surface for easy examination. You can also see multiple parallel lines that happily violate Euclid's 5th postulate.
A coral reef is not only one of nature's visual marvels, it also shows an amazing adaptation to efficiently filter feed water by using the expanded surface area that negative curvature provides.
Is the universe Euclidean?
Most cosmologists believe that if we left the Earth in a spaceship headed out in a fixed direction, then after a very long time, we would come back close to where we started. This is because the universe is thought to be finite but unbounded (like the surface of a sphere). However, this leaves God the choice of geometry. Although the non-Euclidean geometries are logically consistent and are as mathematically significant as the Euclidean, one could ask whether Euclidean geometry is more "true" than the others in the sense that it applies to the space we live in. Is the universe an Euclidean space (ie flat), or does it have negative or positive curvature?
People are so used to thinking in terms of Euclidean geometry that it is hard to step outside this mind-set. Since it took mathematicians thousands of years to do this, don't feel inadequate if non-Euclidean three-space seems abstruse to you - it is! To all intents and purposes the space we live in seems to be Euclidean, ie angles of a triangle are always measured as adding up to 180 degrees and the Pythagorean theorem has yet to fail in practice. However, when we speak about the overall shape of the universe itself, things become problematic. It may be that although the universe appears flat on the human scale it has a very slight positive or negative curvature. If we could measure the angles of a sufficiently large triangle in space we might find the sum to be different from 180 degrees.
Note that it is not an easy matter to perform the equivalent operation on the surface of the Earth, and to thus demonstrate the positive curvature of the world we live on. We would need to draw a large triangle flat on the Earth's surface and to measure its angles sufficiently accurately to note that they add up to more than 180 degrees. It can be done, but it is not a simple matter because of the large scale involved and the fact that the Earth is not a perfect sphere.
Physicists tried to see whether they could detect a cosmic deviation from the Euclidean sum by measuring the angles between distant stars. If the universe weren’t flat then the angles between three stars wouldn’t total to 180 degrees. All measurements, however, revealed the standard 180 degrees and for most of the past century the evidence has pointed to a Euclidean cosmos.
At present (2007), the combination of cosmic microwave background, type 1a supernova observations and mass estimates leads astronomers to suggest that the average curvature of our universe is very close to zero. Astrophysicists favour a flat universe but do not rule out a slight positive curvature. An implication of Einstein's theory of general relativity is that Euclidean geometry is a good approximation to the properties of physical space only where the gravitational field is not too strong.
It has also been suggested that the shape of the universe is akin to a two-holed hyperbolic torus. The WMAP satellite currently taking pictures of the early universe will hopefully provide evidence one way or other in the next few years, so that humanity may at last know the shape of existence itself.