Soler's Fractal Gallery: Three-dimensional fractals
Explanation
In August 2009, Paul Nylander used the work of Daniel White to create the first non-geometric three-dimensional fractal, which is now well known as the Mandelbulb, in hounour of Benoit Mandelbrot. There had been 3D fractals before, such as the Menger Sponge, Apollonian sphere packing and the Sierpinski tetrahedron, but none of these had the richness or organic qualities of common 2D fractals.
These new fractals are three-dimensional because, although they are two-dimensional pictures on the screen, they depict three-dimensional virtual objects that exist in mathematical space, in the same way as a perfect cube exists as a mathematical object. Making three-dimensional fractals is like photographing a sculpture, whereas making two-dimensional fractals is like photographing a painting. With the three-dimensional fractals you can change the angle of view, alter the direction of lighting, move in closer, rotate the object and even penetrate the surface (ouch!).
In other words, these three-dimensional images give flat views, just as photos do, of a three-dimensional world. Moving from the flat plane to solid shapes means a whole new world to explore and I am excited about it. Of course, drawing the images takes forever (about an hour) and requires more fiddling. Getting good colours is also a problem. Someone has to do it, though.
The three-dimensional objects are drawn using a programming technique called ray tracing. It consists of shining a virtual light beam onto the object and putting a dot of colour on an imaginary screen corresponding to how the light comes back to the virtual camera. For a proper explanation have a look at ray tracing explained. As for the mathematics, this is a three-coordinate system called triplex algebra. If you are brave see the maths. Of course, as a user of the program you don't need to worry about any of that. I have made a modest contribution to the maths.
All the fractals here were made using the Visions of Chaos program, which is available at Softology. The program is now free and I highly recommend it. I have written simple instructions for using Visions of Chaos. Although I call all my three-dimensional fractals "mandelbulbs", many of them are actually juliabulbs, ie analogues of Julia sets. Please excuse this lamentable imprecision.
Here is a good explanation of how the mandelbulb was created plus some fine images.
Here are three more movies: Rotating Mandelbrot 1105. Please be patient, as the movie takes about a minute to load. This movie features a julia fractal made using Visions of Chaos with power = 9. It shows the rotation of a three-dimensional fractal, allowing us to see its structure from various angles. It runs for 2,25 minutes. Rotating Mandelbrot 3180. This is similar, but runs for 1,48 minutes. From Chaos to complexity shows the growth in order and complexity of a three-dimensional fractal as the power was varied from -2 to 2 and then to 20. It runs for 1,32 minutes.
These new fractals are three-dimensional because, although they are two-dimensional pictures on the screen, they depict three-dimensional virtual objects that exist in mathematical space, in the same way as a perfect cube exists as a mathematical object. Making three-dimensional fractals is like photographing a sculpture, whereas making two-dimensional fractals is like photographing a painting. With the three-dimensional fractals you can change the angle of view, alter the direction of lighting, move in closer, rotate the object and even penetrate the surface (ouch!).
In other words, these three-dimensional images give flat views, just as photos do, of a three-dimensional world. Moving from the flat plane to solid shapes means a whole new world to explore and I am excited about it. Of course, drawing the images takes forever (about an hour) and requires more fiddling. Getting good colours is also a problem. Someone has to do it, though.
The three-dimensional objects are drawn using a programming technique called ray tracing. It consists of shining a virtual light beam onto the object and putting a dot of colour on an imaginary screen corresponding to how the light comes back to the virtual camera. For a proper explanation have a look at ray tracing explained. As for the mathematics, this is a three-coordinate system called triplex algebra. If you are brave see the maths. Of course, as a user of the program you don't need to worry about any of that. I have made a modest contribution to the maths.
All the fractals here were made using the Visions of Chaos program, which is available at Softology. The program is now free and I highly recommend it. I have written simple instructions for using Visions of Chaos. Although I call all my three-dimensional fractals "mandelbulbs", many of them are actually juliabulbs, ie analogues of Julia sets. Please excuse this lamentable imprecision.
Here is a good explanation of how the mandelbulb was created plus some fine images.
Movies
Here is a movie I made showing a flight into and then out of a juliabulb fractal. Try this movie showing a juliabulb rotating from front to back. I have added large format versions of these movies:
flight and rotation. When you view these, make sure you set the resolution to 720p (not the default 360p) and hit the full screen button (the one with the four arrows). See a rotating mandelbulb in glowing colour. Please hit the two arrow icon (next to the one with 4 arrows) to watch it.Here are three more movies: Rotating Mandelbrot 1105. Please be patient, as the movie takes about a minute to load. This movie features a julia fractal made using Visions of Chaos with power = 9. It shows the rotation of a three-dimensional fractal, allowing us to see its structure from various angles. It runs for 2,25 minutes. Rotating Mandelbrot 3180. This is similar, but runs for 1,48 minutes. From Chaos to complexity shows the growth in order and complexity of a three-dimensional fractal as the power was varied from -2 to 2 and then to 20. It runs for 1,32 minutes.
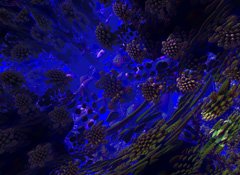
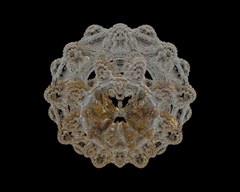
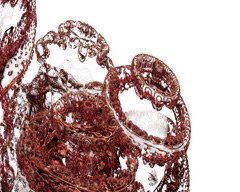
Still images
These are some of the best three-dimensional fractals I have made so far.