A Riddle Called
![]()
Background
The cracking by the Allies of the German
military code called Enigma during World War II is, like the Manhattan Project,
one of the greatest and
most exciting intellectual achievements associated with that conflagration. It
is also credited with shortening the war by two years.
During World War I, German messages had been almost routinely decrypted by the British. The Germans learnt about this years later on the publication of Churchill's book, "The World In Crisis" in 1923. Accordingly, they resolved to make their communications impregnable. The German Army purchased the commercial Enigma machine invented by Arthur Schrebius at the end of World War I and strengthened it significantly. When they began using the military Enigma in 1926, the Germans had the most secure system of cryptography in the world. Because communications during World War II relied much more on radio (as opposed to telephone) than during the First World War, a secure communication system was even more important than before.
Without any knowledge of the inner workings of
Enigma, it seemed impossible to decrypt its messages. Fortunately for the
Allies, a failed businessman called Hans-Thilo Schmidt sold to the French
secret service the instructions for using the machine, including the codebooks
containing the keys for September and October of 1932. Not knowing what to do
with these documents, the French passed them on to the Poles. This made it possible for the Poles, desperate to
stave off a German invasion, to deduce the wiring of the machine, which was a
remarkable feat of mathematics. Although
knowing how the machine worked was an important breakthrough, the task of decrypting
its messages was still daunting. Indeed, the Germans believed it to be
virtually impossible. A German memorandum stated, "It is assumed in
judging the security of the cryptosystem that the enemy has at his disposition
the machine." When they interrogated captured Germans after the War, the
Americans learned that German cryptographers, at least, understood very well
that Enigma messages were not unbreakable. They just found it impossible to
imagine anyone going to the immense effort required.
The Enigma machine and its codes
[If] a man were able to adjust, day
and night, a new key at every minute, it would
take him 4000 years to try all those
possibilities through one after another. - Mid-1920s
Enigma sales brochure.
The Enigma machine was a portable electro-mechanical device with a keyboard much like the familiar qwerty, but with no numbers or punctuation marks. As the operator typed in the clear text of the message to be encrypted, the Enigma showed the encrypted text by lighting up letters, one at a time. Encryption was performed by three rotating disks, called rotors, that scrambled the message, plus a plugboard (which was not present in the commercial Enigma) that swapped six pairs of letters. Each rotor could be set into one of 26 positions, each of which performed a different encryption. Thus there were 26 × 25 × 26 = 16,900 possible ways that the scrambler rotors could rearrange the letters of the alphabet. The first (rightmost) rotor stepped each time a letter was entered, thus changing the encryption every time. A pawl on the first and second rotors caused the next rotor to step forward when it engaged the next rotor's ratchet. The number above is not 26 cubed because of a peculiarity called double-stepping.
Striking a key caused current to pass through the plugboard, changing its path if that letter was plugged to a different letter. It then entered the first, or rightmost, rotor at the input contact. The rotor wiring redirected it to a different output letter, which went directly into the next rotor's input. After passing through, and swapping letters in each rotor, the current entered a reflector. The reflector changed the letter once again and sent the current back through the rotors, causing three more changes. The current made one last pass through the plugboard and finally on to the light panel, where the enciphered letter lit up.
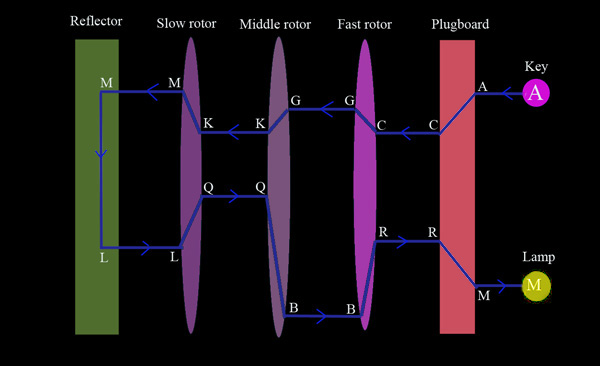
Schematic diagram showing how Enigma enciphered letters. The key A is hit, current takes A to the plugboard, where it is switched to C. It continues on to the first rotor, which encodes it as a G. The middle rotor changes it to K, and the slow rotor changes the K to M. The reflector changes the M to L, which passes again through the three rotors, reaching the plugboard as an R. The plugboard swaps it to M, and this is the light that shines, indicating the enciphered letter. Note that if an M were typed with the same rotor positions, then it would light the A lamp, as it would trace the same path, only in reverse.
It has been estimated that 100,000 Enigma machines were constructed by the end of the War. Presently, Enigma machines are on display in museums around the world, including in our very own Power House.

A three rotor German military Enigma (photo: Karsten Sperling)
Every day there was a new day key, which was
specified for the month ahead in a code book. This key, which was used for only
one day, consisted of:
a) the plugboard settings, ie the
six pairs of
letters that were swapped, eg A for L, B for G, P for S, V for D, W for T, and Z for Q.
The swaps were reciprocal.
b) the order of placement of the three rotors,
giving 6 possibilities. In 1938 the number of rotors was increased to five,
though only three were used at any one time, giving 60 possible ways of
arranging the rotors.
c) the orientation of each of the three rotors,
ie the letter that was facing upwards in each, eg Q-C-T.
d) the position of the rotor notches, which controlled the stepping of the second and third rotors.
Part of a code book (photo: Ben Slivka)
The reflector connected the outputs of the last rotor in pairs, redirecting current back through that rotor by a different route. Unlike the rotors, the reflector always made the same letter swaps. The reflector ensured that Enigma was self-reciprocal: conveniently, encryption was the same as decryption. However, the reflector also gave Enigma the property that no letter ever encrypted to itself. This was a severe conceptual flaw and a cryptological mistake subsequently exploited by codebreakers. Enigma messages were sent using Morse code.
To see why the reflector caused encryption to be the same as decryption and each letter to encrypt to a different letter, consider the last rotor, ie the one before the reflector. Suppose that at its present setting it changes the letter K to the letter M. The reflector would change the M to say L. When L was passed back to the last rotor, it could not be changed to K because K was connected to M in that rotor in both directions. The same applies to passing back through the other two rotors and the plugboard - all are symmetric. Hence each input letter emerged as a different letter after passing through Enigma. It follows from this that encryption is the same as decryption, because if A passed through all the connections to come out as M, then M would pass through all the same paths, but in reverse, to emerge as A.
What made the system much more secure was that the day key was only used to encrypt another key, called the message key. The operator would select a new and arbitrary message key for each new message. This consisted of a new orientation of the three rotors. The message key was sent encrypted by the day key. Due to concern about static and operator error, the message key was sent twice. The procedure was that the operator would set up his Enigma each morning according to a) through d) as specified for that day in the code book. He would then select a three-letter key at random and encrypt it using the agreed on settings of the machine, using the day key part c), say QCT. This would be sent twice, as six letters. Thus the message key D-P-L might be sent as F-O-K-H-T-R. Note that DPL is encrypted as FOK the fist time then as HTR. This was because one of the rotors would step to a different orientation after each letter. The sender then changed the orientation of his three rotors from QCT to DPL. The receiver would type FOKHTR into his machine and obtain the clear text DPLDPL. Recall that Enigma was symmetric - the encryption process was the inverse of decryption. The receiver would then set his rotors to DPL. The message encrypted under DPL could now be sent and decrypted at the other end. To increase security, individual messages were supposed to be shorter than 250 letters (though this was not always observed), so that a long message would be sent as a number of short encrypted texts, each encrypted under a different message key.

Enigma plugboard
showing two swaps: A-J and S-O (photo: Bob Lord)
The Enigma in context
The most elementary kind of cipher, which had
been used by Julius Caesar, is the monoalphabetic one. In such a cipher, each
letter is changed to another letter according to a single mapping, eg A goes to
C, B goes to Q and so on. This translation does not change. A more
sophisticated cipher, the polyalphabetic one, relies on the same principle but
uses multiple mappings. Thus A may go to C at one point but later it may be
changed instead to F. In effect, a polyalphabetic cipher cycles through a
number of monoalphabetic ones. This greatly increases security, as a
straightforward frequency attack, based on the known frequencies of occurrence
of the letters in the language, cannot break such a cipher.
The Enigma, and other similar rotor machines, was a mechanised version of a polyalphabetic cipher. Using three single-notched rotors, the period was 16,900, long enough to prevent any detectable repetition in the enciphering sequence. The feature of the Enigma that made it have such a long period, ie the interval before the same translation came into effect, was the stepping of the three rotors. The first rotor stepped every time a key was pressed, resulting in a different cryptographic substitution. The middle rotor also advanced one position when the notch on the first rotor engaged with a position on the middle rotor. This happened when the first rotor completed a revolution ie 26 steps. Likewise for the third rotor. If the rotors had not stepped then the combined effect of the three rotors would be a single substitution, ie a monoalphabetic swap, though this would have been different for each message, due to the use of a different message key for each transmission. In other words, there would have been no point in having three rotors if there were no stepping mechanism.
The
Enigma system was a formidable challenge for the cryptanalysts due to the huge number of possible keys, which was
of the order of 1020
The Poles break Enigma
A Polish cryptanalist called Marian Rejewski led a team of mathematicians charged with the task of breaking Enigma. Being a mathematician, he was skilled in finding patterns. He wrote, "Whenever there is arbitrariness, there is also a certain regularity. There is no avoiding it." The repetition of the message key was a weakness of the Enigma system and was the starting point of Rejewski's attack. Specifically, there was a relationship between the first and fourth letters of the initial six-letter message, as well as between the 2nd and 5th, and the 3rd and 6th. If he got enough intercepted messages Rejewski could compile a table of correspondences between the first and fourth letters under the current day key, eg the letters abcdefghijklmnopqrstuvwxyz would be turned into qaweszxdrtfcvgyuhbnjiokmlp. He would compile similar tables using the 2nd and 5th positions, and the 3rd and 6th. Rejewski looked for patterns in these tables and focused on cycle length. Thus B might be encrypted as G, G as F, F as R and then R as B, completing a cycle of length 5. The length and number of cycles was different each day and was a characteristic consequence of the day key.
Marian Rejewski circa 1932 Rejewski now had a profound insight: the number
of links in the cycles is purely a consequence of the rotor settings, ie it is
independent of the plugboard cabling. This made his task a hundred billion
times easier, though there were still 105,546 rotor settings to be checked. Note
that 105,546 = 17,576 rotor orientations
times 6 possible rotor placements. Using replicas of the Enigma units and a machine of his own invention, called
the Cyclometer, his team took a year to catalogue the cycle lengths for each of
these 105,546 rotor settings. Once he had this catalogue, Rejewski would look
up the patterns made by the day key, allowing him to find the correct
arrangement and orientation of the three rotors. Next he needed to
identify the plugboard settings. To do this, Rejewski set his Enigma to the rotor
settings corresponding to the day key and unplugged the plugboard, so that it
had no effect. He fed cipher text into the machine, obtaining mainly gibberish,
since the plugboard cablings were missing. However, occasionally snatches of
recognisable phrases would appear, eg "mnucheu", which was probably
"Munchen" (Munich in German). This would lead him to conclude that
the letters n and u should be swapped but that the letters m, c, h and e should
not be changed. Using this method, he was able to identify the six pairs of
interchanged letters before the day was out, usually in a matter of about
fifteen minutes. Once
the correct wiring positions were found, it was easy to find the day's position of the
stepping notch of the rightmost rotor. After at most 25 steps, Rejewski
would get gibberish. All he had to do then was to try at most 25 positions to
see where the notch should be to get a correct continuation of the message. If
the fast rotor also stepped in the message (somewhere between 26 and 676
characters) then Rejewski tried out all 26 possible notch positions of the
middle rotor. So the stepping of the rotors did not pose any real problems once
the other parts of the day key were known. At this point Rejewski could decipher any message sent that day, as
if he had been given the settings a), b), c) and d) above. Note that Rejewski
assumed that the rotors did not step during the repeated sending of the message
key. The rotors did step roughly every fourth message, causing his method to
fail in these cases. The
repetition of the message key was a blunder. If the Germans had sent the message
key exactly duplicated, ie as FOKFOK, instead of FOKHTR,
as in the above example, then Rejewski's attack would have had nothing to work
on. It took the German cryptographers until 1940 to rectify their error. 
The Poles successfully decrypted Enigma in 1932. However, it is important to bear in mind that Enigma was
a work in progress, ie it changed during the course of the war, with the
code-breakers being forced to play a game of catch-up. Although the Germans
believed it to be unbreakable, they nevertheless repeatedly improved it to
remove some of its weaknesses and to make it more complex and hence more
secure. Moreover, the cryptographic situation during the war was more
complicated than can be covered in a short article. There were different
versions of the Enigma system being used at the same time, eg different keys
were being used in different geographical areas, as well as different versions
of the machine itself being used by the various branches of the German
military. In particular, the marine Enigma (crucially used by the U-boats, the
German submarines) was different from and significantly
stronger than that of the army, which is the subject of this article. There was
also another cipher, used for the most important high-level messages, called
the Lorenz SZ 40. This used an entirely different machine, which was less
portable. The Lorenz code was also broken by the British. To do so they created the
Colossus,
the world's first electronic digital computer, but that is another major story.
In September 1938, the Germans ceased using a fixed setting of the three
rotors for each day. The new method was that the sender set his machine
according to parts a) b) and d) of the day key and selected two random
sequences, eg WZA and SXT. He then set his Enigma to WZA and encoded SXT,
giving UHL. He sent WZA in the clear, UHLZAS (SXT encoded twice using WZA) and the message
itself encrypted under SXT. At the other
end, the machine was set to WZA, allowing decryption of UHL to give SXT. This
setting would then be used to decrypt the message. The change
eliminated a major weakness of the Enigma system: the use of the same daily setting for all messages, making subsequent
cryptography considerably harder. Note that although WZA was sent in the clear the
Poles could not decode UHL to
get SXT using WZA because they did not know the day key, which now comprised a), b) and d).
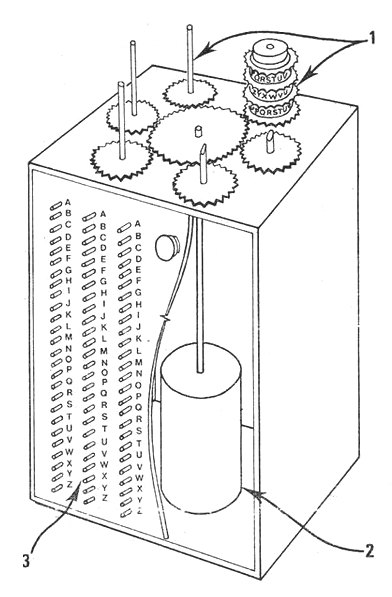
This change immediately invalidated Rejewski's method. Rejewski retaliated by inventing the "cryptologic bomb" or bomba. This was a machine composed of six Enigmas, designed to perform an exhaustive, ie brute force, analysis of the 105,456 possible rotor settings in order to obtain the day key. Six bombs were used simultaneously, one for each possible arrangement of the three rotors in the Enigma. It now took about two hours to find the daily key. It may have been called a bomb because it made a ticking noise.
Rejewski's cryptologic bomb: 1 Rotors 2 Electric motor 3 Switches
(Courtesy of Janina Sylwestrzak, Rejewski's daughter) In December 1938, the German army again stepped
up security by increasing the possible rotors from three to five, though only
three were used at any one time. This increased the number of possibilities to
be checked by a factor of ten. To make decryption even harder, the number of
plugboard letter swaps was increased to ten (whereas the optimal number is
eleven). Although these quantitative
improvements did not invalidate the methods used by the Poles, they made
decryption largely impractical, due to the Poles' limited machinery and
personnel.
The
Polish gift on the eve of war
On 24 July 1939, just five weeks before the outbreak of war, the Poles handed over to the British and French authorities two Enigma replicas and all of their findings, which they had kept secret until then. The British had believed Enigma to be invulnerable for thirteen years, but now they were given a head start by the Poles, who had proved that the code was breakable. Equally importantly, the Poles provided the wiring of the rotors. The story of the breaking of Enigma resumed in Britain, at Bletchley Park, where eventually seven thousand people laboured on deciphering the German codes.
The
British attack Enigma
Traditionally, the British cryptography office had been manned by linguistics and classic scholars, crosswords afficionados and the like. World War II marked a turning point in that the British now engaged mathematicians and scientists in much greater numbers. Having assimilated the Polish methods and possessing much greater resources, the British were able to break each new day key within a matter of hours. They found additional ways of exploiting the weaknesses of the system by focusing on its most vulnerable side - the human factor. The first of these vulnerabilities was what came to be known as cillies. The German operators were supposed to choose random letters for each message key, but in some cases they inadvertently picked an obvious sequence, such as BNM, ie three consecutive letters on the German keyboard. They also used names, such as hitler and berlin, as well as German obscenities. Another operational error was the repeated use of the same key, such as CIL, believed to be the initials of a girlfriend. This may have given rise to the term cillie. Cillies were also produced by the tendency on the part of the encipherer to take the final rotor setting of one message as the initial setting of the next. Part of the problem from the German point of view is that human beings are not very good at generating random patterns. Rejewski wrote, "...it is a well-known phenomenon that man, as a being endowed with consciousness and memory, cannot imitate chance perfectly, and it is the cryptologist’s task, among other things, to discover and make proper use of these deviations from chance."
Another weakness of the system which the British uncovered was that the compilers of the code books decided not to allow any of the rotors
to be in the same position for two days in a row. This had the unintended
effect of reducing by half the number of rotor settings that the British needed
to check. Another German error was the rule that plugboard settings could not
include a swap between two adjacent letters, ie G could not be changed to F or
H. Once they discovered this restriction decryption became much easier for the
British.
However, this was not the end of the story. The British were obliged to look for new methods because Enigma continued to evolve, right till the end of the War. In particular, they foresaw that the Germans would eventually realise that the repetition of the message key was a weakness of the system. Once the Germans ceased repeating the key a new method of decryption would be needed. The British were fortunate to have among their cryptanalysts a mathematical genius called Alan Turing. After studying the large collection of previously decrypted messages, Turing found that he could predict part of the content of an undeciphered message purely based on where and when it was sent. For example, the Germans sent a weather report shortly after 6 am every day. Such a message was almost certain to contain the word "wetter" (weather). In addition, the rigid military mindset ensured that messages often adhered to a regimented format, including the repetition of long titles, such as Obersturmbannfuhrer. Turing found that 90% of German messages contained the word "eins" (one), prompting him to create an eins catalogue, an alphabetic list of 17,576 ways of enciphering this word. When a piece of clear text can be associated with an encrypted message it is called a crib. It was known from call signs and direction finding what organisations (ground forces, air forces, Abwehr or navy) originated the messages and from what locality. This helped with cribs.
A fruitful source of cribs were re-encipherments of messages that had previously been decrypted either from another Enigma network or from a lower-level manual cipher. This happened particularly with German Naval messages being sent in an insecure Dockyard cipher and repeated verbatim in an Enigma cipher. Occasionally, when there was a particularly urgent need to break the German Naval code, such as when an Arctic convoy was about to depart, mines would be laid by the RAF in a defined position whose grid reference in the German Naval system was known to the British. The warning message about the mines would be transmitted both on the dockyard network and on the U-boat network. The process of planting a crib was called gardening.
The Abwehr was the intelligence and
counter-espionage service of the German High Command. It placed espionage
agents in enemy countries. These spies inevitably used a lower level cipher for their
transmissions, perhaps due to the limited portability of the Enigma. This lower
level cipher was broken by Oliver Strachey's section at Bletchley Park. The messages were often then re-transmitted word-for-word
on the Abwehr's internal networks using Enigma, which gave the best possible
crib for deciphering that day's Enigma key. Interception and analysis of
Abwehr transmissions led to the remarkable state of affairs in which a
categorical assurance was given by MI5, that all the German spies in Britain
were controlled as double agents working for the Allies under the Double Cross
System. A related operational weakness was that when the Germans increased their
security, such as going from three to four rotors for the naval Enigma, this was
deployed incrementally, ie the same message was sent using both the old and new
method, since not all units had yet switched to the stronger code. This allowed
the Allies to work out the wiring of the new rotors.
Although cribs were no more than intelligent
guesses, they became the central tool of the cryptanalysts. Yet it required
great ingenuity to exploit them. Even if it were known that a particular piece
of coded text corresponded to a known crib, it was a far from trivial task to
work back from this to recover the day key. In fact, the straightforward way to
do this would require checking which of 1020 settings of the Enigma
would produce the crib, which was obviously impracticable. A stroke of genius
was called for. 
Turing's bombe
To simplify finding the Enigma settings that enciphered a given crib, Turing followed Rejewski's strategy of isolating the effect of the configuration of the rotors from that of the plugboard. Once this was achieved, it would suffice to check each of one million possible rotor settings (ie 60 choices of rotors, each with 17,576 possible orientations). This was a feasible task using 1940s technology. Then the plugboard cablings could be deduced using Rejewski's method. Turing's new idea was to exploit the existence of loops in the encryption of cribs. Suppose that the crib "wetter" is believed to correspond to the cipher text "ETJWPX". This gives rise to a three element loop. At Enigma setting T the letter w is encrypted as E, at Enigma setting T+1 the letter e is encrypted as T, and at Enigma setting T+3 the letter t is encrypted as W, completing the loop. Note that the first 't', the 'e' and the 'r' are not part of the loop and hence are ignored.
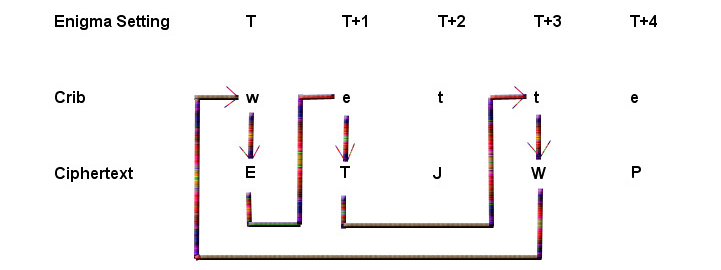
To exploit such a loop, Turing conceived of
linking three Enigma machines, identically configured except that the second
machine would have the rotor settings advanced one place and the third with
settings advanced three places. The three Enigmas were electrically connected
so that the output from each became the input of the next. This electrical loop
mirrored the loop between the crib and the cipher text described above. When
each machine made the correct translation ie w -> E for the first, e -> T
for the second and t -> W for the third, then the circuit would be completed
and current would flow, causing a bulb to light. Crucially, the plugboard
cablings could be ignored because they cancelled themselves out. This was
because the plugboard made its swap both before and after the letter was passed
through the rotors inside each Enigma. So when the output from the rotors of an
Enigma passed through that Enigma's plugboard on the way out, this swap was
reversed when the encrypted letter passed through the plugboard of the next
Enigma on the way in. So only the effect of the rotors needed to be taken into
account. Since the plugboard settings were irrelevant this decreased the number
of possibilities by a whopping 1014.
It was assumed when using the
bombe that for a small stretch of letters
only the fast rotor moved, and that the other two remained stationary.
However, all 26 outputs of the first set of
rotors had to be connected to all 26 corresponding inputs in the second set,
and so on. So there were 26 electrical loops, each with a light bulb to signal
a match. Because the plugboard settings cancelled themselves out, only 17,576
orientations of the rotors needed to be checked. However, it was still necessary to try
all the possible choices and arrangements of the rotors, ie sixty in all. This
could be achieved by running sixty sets of three Enigmas simultaneously.
Following Rejewski’s precedent, Turing called his invention a “bombe”.
One of the weaknesses of the Enigma was that the plugboard connections were reciprocal, so that if A was plugged to N, then N likewise became A. This property inspired mathematician Gordon Welchman at Bletchley Park to propose that a diagonal board be introduced into the bombe. By increasing the number of feedback connections it substantially speeded up the process of elimination. Turing's bombe looked for all the rotor settings that allowed the cipher to match the assumed plain text. The moment that each position made contact, an electrical current tried to complete a path. Most combinations could not complete the path correctly and were discarded. Those that did complete the path caused the machine to stop. Gordon Welchman wrote that the task of the bombe was simply to reduce the rotor order and positions that required further analysis to a manageable number.
Like the Polish Bomba, the machine Turing
devised also ran through all the possible rotor settings. Drums and wires simulated a series of Enigma rotors.
However, rather than looking for the one correct rotor setting based on the repeated key, as the Bomba did, Turing's looked for all
the rotor settings that allowed the cipher to match the crib. Or,
more correctly, it searched all the settings and disregarded those that were
incorrect. For example, if the crib letter was G and the
corresponding cipher letter was L, Turing's test register ignored
any results that did not allow the electrical current to pass from G to L. By disproving thousands of rotor settings,
those left were possible correct settings. The bombe positions at the possible true stops were then tried out
on Type X machines that had been adapted to mimic Enigmas. All of them would correctly decipher the
crib, but only the true one would produce, after all the plugboard settings had
been found, the correct plaintext. It was not hard to find the plugboard
settings because comparing the encryption of the crib
without any plugboard swaps with the actual ciphertext would show the swaps for
a number of letters (ie for all the letters in the crib). The rest could be worked out by looking at the message
after it was decrypted using the known plugboard swaps.

