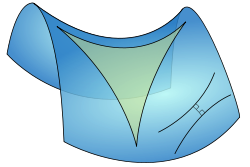

A triangle immersed in a saddle-shape plane (a hyperbolic paraboloid), as well as two diverging parallel lines.
Working in around 300 BC, the Greek mathematician, Euclid set geometry on a firm logical footing by establishing his five axioms and using these to prove geometrical theorems. Euclid's book, "The Elements", was probably the most important and influential textbook ever written, as well as the most enduring. However, many mathematicians harboured doubts regarding Euclid's 5th axiom, the one about parallel lines. It is more complex than the others. Unlike the first four postulates, the 5th is not immediately obvious to our intuition. Over the intervening centuries many tried to derive the 5th axiom from the first four. Others tried to prove the postulate by assuming its negation in the expectation that they would produce a logical contradiction. Both these endeavours failed. The reason they failed is that Euclid's 5th postulate is neither true nor false.
Until about 1830 AD it was believed that Euclidean geometry was identical with geometry, and with truth. Today, however, many other self-consistent non-Euclidean geometries are known, the first ones having been discovered in the early 19th century. It also is no longer taken for granted that Euclidean geometry describes physical space. An implication of Einstein's theory of general relativity is that Euclidean geometry is a good approximation to the properties of physical space only if the gravitational field is not too strong.
Hyperbolic geometry (also called Lobachevskian geometry or Bolyai-Lobachevskian geometry) is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced. The parallel postulate in Euclidean geometry is equivalent to the statement that, in two dimensional space, for any given line l and point P not on l, there is exactly one line through P that does not intersect l; ie, that is parallel to l. In hyperbolic geometry there are at least two distinct lines through P which do not intersect l, so the parallel postulate is false. Models have been constructed within Euclidean geometry that obey the axioms of hyperbolic geometry, thus proving that the parallel postulate is independent of the other postulates of Euclid.
Hyperbolic geometry can be characterised by the fact that hyperbolic triangles (the natural analogue of a usual Euclidean triangle in a hyperbolic space) have angles which total less than 180°. There are even hyperbolic triangles in which all three angles are 0°.
Hyperbolic geometry is not the only alternative to Euclidean geometry. There is also the geometry of positive curvature, where triangles add up to more than 180 degrees.
"The Poincare conjecture and Perelman's proof of it is one of the greatest achievements of our age; it tells much about the possible nature and shape of our universe." Perelman used the Ricci flow equation in his proof. "The Ricci flow equation treats the curvature of space as if it were an exotic type of heat, akin to molten lava, flowing from more highly curved regions and seeking to spread itself out over regions with lesser curvature."
Important definitions: For each positive integer n, an n-space is the set of all ordered n-tuples of real numbers. Euclidean space of dimension n is n-dimensional space with distance defined by the Pythagorean Theorem. A manifold is a mathematical set that looks like Euclidean n-space at each point ie locally, but not necessarily globally.
A surface is a two-dimensional manifold. Thus a sphere (which is a 2-manifold) is not equivalent to a plane. Although small areas of the sphere can be mapped onto a plane surface, the overall sphere cannot. This is why no flat map can represent the surface of the Earth without distortion. On the other hand, we can usually get by in our lives pretending the Earth is flat.
"If every loop on a manifold can be shrunk to a point, we say that the manifold is simply connected. The sphere is the only simply connected two-dimensional manifold, a mathematical set that looks like Euclidean space at each point. Regions sufficiently near any point are homeomorphic to n-space. N-space is the set of all ordered n-tuples of real numbers. A homeomorphism is a one-to-one correspondence between two manifolds in which nearby points correspond to nearby points."
The Poincare Conjecture states that the only compact (finite) three-dimensional manifold without a boundary in which every loop can be shrunk to a point is a three-sphere. Given that the conjecture has been proved, we can say for sure whether our universe is a three-sphere by using a complete atlas of the universe to check whether every closed loop can be shrunk to a point.
"... it is virtually certain that the universe, just like the surface of the Earth, curves differently in different places."
"To say that the universe has no boundary is not to say that it goes on indefinitely, just as to say that the Earth has no edge is not to say that it goes on forever... It may be that the universe goes on for ever, but it seems very unlikely. Space and matter are intimately related, and the assertion that the universe has an infinite amount of matter causes serious theoretical problems... If we left the Earth in a very fast spaceship, headed out in a fixed direction... after a very long time, most cosmologists and mathematicians believe, we would come back close to where we started."
Before it was known that the earth is a sphere the candidates for the shape of the surface of the Earth would be the various two-dimensional manifolds, such as a torus or a sphere. The corresponding mathematical object that models our universe is a three-dimensional manifold, or three-manifold. It is a set in which every point belongs to a region that can be mapped onto the points inside a shoebox. So the region around every point looks like a space rather than a plane.
Two three-manifolds are the same topologically if the points of one can be put into a continuous one-to-one correspondence with the points of the other. "Continuous" captures the notion that nearby points correspond to nearby points. Two such manifolds are said to be homeomorphic.
To imagine a three-sphere, think of two solid balls. Each is bounded by its spherical surface. Now picture the two balls as being glued together along their boundaries. In other words, the surface of one ball is deemed to be identical with the surface of the other (don't try this at home!). The resultant three-sphere has no boundary. If one leaves one of the balls one enters the other, with no edge or seam to mark the transition. Equivalently, a three-sphere is the set of all points at a fixed distance from a point in 4-dimensional space, or to put it another way, a 3-sphere is an object with three dimensions that forms the boundary of a ball in four dimensions. A three-sphere has constant positive curvature.
The unsuccessful efforts to prove the fifth postulate of Euclid in the 18th century resulted in the understanding that many results are equivalent to it. Four results equivalent to the 5th postulate are:
Given a line L and a point P not on the line, there is precisely one line through P in the plane determined by L and P that does not intersect L.
The sum of the angles in a triangle is 180 degrees.
The ratio of the circumference to the diameter of a circle is the same for all circles, no matter of what size.
The Pythagorean Theorem
Other geometries, in which the 5th postulate does not hold exist. But these other geometries are not logical curiosities, anomalies springing from the failure of the first four postulates to adequately capture reality. These other geometries are every bit as real and as valuable as the familiar plane geometry. They simply describe a different place - not the flat plane but the surface of a sphere or torus.
We define straight lines (geodesics) as those that travel along the shortest distance between their points. To the inhabitants of a space, these are the lines that appear straight. A triangle is the figure bound by three geodesic segments. Triangles allow us to define curvature. Positive means triangles have more than 180 degrees, negative curvature less than 180 degrees, and zero curvature that the triangles have angle sum exactly equal to 180 degrees. This is the definition of mathematical curvature.
Two-space is the set of pairs of real numbers. It becomes Euclidean two-space if we define the distance via the Pythagorean theorem. Once we define a distance we have straight lines. If we define distance using the Pythagorean Theorem then we get the "Euclidean package". However, there is nothing god-given about this - other notions of distance are equally valid.
Riemann showed that every surface in ordinary Euclidean three-space has a metric, hence straight lines. A surface with a metric is called a geometry. It inherits the metric from the space in which it sits. This is why we can talk about geodesics on the surface of a sphere or a torus.
On a sphere such as our Earth, geodesics are so-called great circles, each having the same diameter as the sphere. Beijing and Philadelphia are on the same latitude. If we travelled from one to the other along the same latitude, we would go 10,130 miles. However, a geodesic between the two cities, which passes close to the North Pole, is only 6,878 miles. Yet on a flat map of the Earth the path along the line of latitude would appear straight. This is because maps of the world on flat paper necessarily distort distance.
Take two lines of longitude coming from the North Pole plus the segment of the Equator between them. The two base angles are both right angles, so the sum of the angles in this triangle is more than 180 degrees. Hence geometry on a sphere has positive curvature. There are no parallel lines on a sphere as all great circles cross one another. To see this, imagine one great circle, which cuts the sphere into two equal parts. Any other great circle cannot remain within one of these two halves. If it did, its diameter would be less than that of the sphere.
Surfaces in three-space that have a saddle shape have negative curvature. Equivalently, triangles on such surfaces have angle sum less than 180 degrees. Conversely, any negatively curved surface in three-space must be saddle-shaped everywhere. In contrast to the sphere, whose triangles seem to bulge out, on a saddle a triangle whose sides are geodesics seems sucked in. A tiny being living on either surface would view the lines as perfectly straight, and would only be able to tell whether the triangle was bulging or sucked in by measuring its angle sum.
On a positively curved surface the area of a circle is less than pi times the square of its radius. On a negatively curved surface, the area is less than pi r2. On a negatively curved surface if we start out from two nearby points along geodesics that appear to be parallel, the lines will diverge because there is more surface. The opposite is true on a sphere, causing all potential parallels to intersect.
In topology, two spaces are considered the same if there is a homeomorphism between them. A homeomorphism is a one-to-one correspondence between them so that nearby points are mapped to nearby points. Yet two surfaces that are the same from a topological point of view can look very different from a geometric point of view. For instance, a sphere and the surface of a long thin cigar are topologically equivalent. A homeomorphism between a sphere and a cigar shape does not preserve distance. If two surfaces are geometrically equivalent (isometric) then there is a mapping between them such that points that start out being exactly a millionth of an inch apart are mapped to points that are also exactly a millionth of an inch apart.
A homeomorphism can be visualised as if the first surface were made of rubber and were stretched to fit over the second surface. On the other hand, a geometric equivalence, or isometry, can be visualised as the first surface being made of a flexible but not stretchable material and draping it over the second surface. Thus a rectangle of cloth can be used to perfectly wrap a cylinder, which is flat. On the other hand, a sphere is not flat, so that a sheet cannot fully cover it without wrinkling.
One can imagine a clever tailor fashioning a piece of cloth that will fit perfectly over a beachball. The cloth would have to have less area inside a circle of fixed radius than on a bedsheet. To do so they would need to cut out darts from the fabric and then sew it together again. The resulting piece of cloth would be isometric to a sphere. One would have to crease a piece of positively curved cloth to lay it on a dresser.
In contrast to a sphere, the saddle-shaped area on a woman's side above her hip has negative curvature. To drape this part of her body exactly a cloth with negative curvature is required. The region inside a circle of a given radius contains more material than the same circle in a plane. To make suitable cloth a tailor might start with a flat piece of fabric, make a cut as if to make a dart, but instead of stitching the cut edges together, insert an extra piece of fabric. Negatively curved cloth would have lots of folds if one tried to lay it flat on a dresser.
Riemann provided a context in which non-Euclidean geometry seemed as natural as Euclidean, both appearing as special cases in a much broader conception of geometry. Riemann made the important distinction between physical and mathematical reality. A mathematical object exists if it is well defined even though it may not appear in our familiar three-dimensional space.
Any surface can be given a (unique) geometry in which it has constant curvature. The curvature of a manifold is the deviation of the sum of angles of triangles from 180 degrees.
The effect of connecting the bottom and top edge of a square sheet of paper is to roll it into a cylinder. This does not distort distances ie straight lines drawn on the square remain straight lines on the cylinder, which has zero curvature. Triangles on the cylinder still add up to 180 degrees and the cylinder is mathematically flat. You can easily wrap a sheet around a cylinder. However, once we connect up the ends of the cylinder together to form a torus, distances are distorted and curvature is introduced. This is because the paper would be compressed in some places and stretched in others, unlike in the first operation. The curvature on the surface of a torus varies from positive, through zero to negative.
The usual two-dimensional sphere (ie a spherical surface) is the set of points at a fixed distance from a given point in Euclidean three-space. The three-sphere is the set of points at a fixed distance from a given point in four-dimensional space. Hence it is not something that can be created in our space.
People are so used to thinking in terms of Euclidean geometry that it is hard to step outside this mind-set. Since it took mathematicians thousands of years to do this, don't feel inadequate if non-Euclidean three-space seems abstruse to you - it is! To all intents and purposes the space we live in seems to be Euclidean, ie angles of a triangle are always measured as adding up to 180 degrees and the Pythagorean theorem has yet to fail in practice. However, when we speak about the overall shape of the universe itself, things become problematic. It may be that although the universe appears flat on the human scale it has a very slight positive or negative curvature. If we could measure the angles of a sufficiently large triangle in space we might find the sum to be different from 180 degrees.
Note that it is not an easy matter to perform the equivalent operation on the surface of the Earth, and to thus demonstrate the positive curvature of the world we live on. We would need to draw a large triangle flat on the Earth's surface and to measure its angles sufficiently accurately to note that they add up to more than 180 degrees. It can be done, but it is not a simple matter because of the large scale involved and the fact that the Earth is not a perfect sphere.
So it is perfectly legitimate ask whether the universe we live in is an Euclidean space (ie flat), or whether it has negative curvature (hyperbolic space) or has positive curvature. At present (2007), the combination of cosmic microwave background, type 1a supernova observations and mass estimates leads astronomers to suggest that the average curvature of our universe is very close to zero. Astrophysicists favour a flat universe but do not rule out a slight positive curvature.
"Artists and humanists embrace complexity and ambiguity. Mathematicians, in contrast, work by obsessively defining terms and stripping off extraneous meaning. The almost neurotic insistence that every term be rigorously defined, and every statement proved, ultimately frees one to imagine and talk about the unimaginable. Most people, traumatised by school experiences of mathematics, know only too well that mathematics is the most meticulous and demanding of disciplines, but few get to see that it is also the most liberating and imaginative of all human activities. Absolute precision buys the freedom to dream meaningfully."
Hyperbolic space is not something that we can perceive directly. However, various models that give us a feel for its properties can be constructed. Going down one dimension, we can show what a hyperbolic surface looks like eg a saddle shape. The crocheted coral reef is an attempt to give a feel for hyperbolic 3-dimensional space within our familiar framework of Euclidean space. The crocheted reef is a hyperbolic surface made of negatively curved cloth.
Material taken from the website of the Institute for Figuring at http://www.theiff.org/oexhibits/oe1.html
In reality, hyperbolic space is infinitely large. Like the Euclidean plane it goes on forever. But in order for us to depict it within our Euclidean framework we have to make some compromises. The Poincaré compromise is to represent angles truly while distorting scale. In this diagram all the sides of the green areas are, in fact, of equal length.

In his book Science and Hypothesis (1901), Poincaré wrote of his model as an imaginary universe. To us, as observers of this bubble world, the inhabitants of the disc appear to shrink as they approach the boundary of the disc. They, however, see no such effect. As far as they are concerned, they live in a perfectly normal non-shrink space, albeit one that is not Euclidean. It is only we, confined to view them in an Euclidean framework, who see their dimensions behaving strangely.
We can cover the Euclidean plane with hexagons so that each is surrounded by six others and they all fit neatly together to exactly fill the space. To make a soccer ball, we replace some of the hexagons with pentagons (which only have five sides), thereby causing the now fewer number of hexagons to close up towards one another and wrap into a sphere. This is how a soccer ball is made.
To make a hyperbolic model we make the opposite move. Rather than replacing some of the hexagons with pentagons, we replace them with heptagons (which have seven sides). Now, instead of closing up, the surface opens out – for the heptagons add to, rather than subtract from the space, and what we get is an excess of surface. The effect is similar to what we see in lettuce leaves and certain types of kelp where the vegetable surface expands outward from a modest start, generating a ruffled effect.
In 1997 mathematician Daina Taimina worked out how to make a physical model of hyperbolic space that allows us to feel, and to tactilely explore, the properties of this unusual geometry using crochet. The essence of the hyperbolic construction can be implemented with crochet simply by increasing the number of stitches in each row. As you increase, the surface naturally begins to ruffle and crenellate.
Many of the intrinsic properties of hyperbolic space become visible to the eye and can be directly experienced by playing with the models. Geodesics – or straight lines – on the hyperbolic surface can be sewn onto the crochet surface for easy examination. You can also see multiple parallel lines that happily violate Euclid's 5th postulate.
As the rate of increase of the stitches increases, the construction becomes increasingly crenellated. In effect the space around any point expands ever more exponentially. Whereas all spheres have the same form - varying only in size - hyperbolic surfaces may differ dramatically from an external point of view. Mathematically speaking, we characterize this quality by the radius of the hyperbolic plane: the more crenellated the surface appears, the smaller its radius; the flatter the surface, the greater its radius. A regular Euclidean plane can be seen as a hyperbolic plane of infinite radius. The radius of any given hyperbolic plane is the radius of a circle that would sit flatly on a tabletop.
In the late nineteenth century physicists tried to see whether they could detect a cosmic deviation from Euclidean norms by measuring the angles between distant stars. If the universe weren’t flat then the angles between three stars in a triangular configuration wouldn’t add up to 180 degrees. If the universe were spherical, the angles would sum to more than 180 degrees; if it were hyperbolic, they would sum to less. All measurements, however, revealed the standard 180 degrees and for most of the past century the evidence has pointed to an Euclidean cosmos.
In the past twenty years cosmologists have speculated that the universe may be finite but without any boundary, in analogy with the surface of the Earth. One possibility is a finite hyperbolic universe.
You can imagine a finite Euclidean space by regarding as identical the opposite ends of the edges of a square piece of paper. First an edge is joined to the one opposite, creating a cylinder. To join the ends of the cylinder we need to imagine stepping into an extra (ie 4th) dimension, as we do from two to three dimensions in the case of the first join. The end result of the two joins is a "flat" torus (no curvature), a finite Euclidean surface with no boundaries. Regrettably, this cannot be pictured. This flat torus is not to be confused with the physical construction of a torus, in which case curvature is introduced. We can do a similar feat using hyperbolic paper, or better, cloth. The result (trust me) is a two-holed torus, which is a hyperbolic shape.
It has been suggested that the shape of the universe is akin to a two-holed hyperbolic torus. Note, however, that the universe is three-dimensional, whereas the crocheted shapes are merely two-dimensional hyperbolic surfaces that we exhibit within our familiar Euclidean framework. The WMAP satellite currently taking pictures of the early universe will hopefully provide evidence one way or other in the next few years, so that humanity may at last know the shape of existence itself.